Synopsis
Dans cette vidéo, découvrez les deux preuves fournies par Aristote pour prouver que la Terre est une sphère, et comment Ératosthène a calculé la circonférence de la Terre il y a près de 2.300 ans !
Découvrez les notions importantes de l’épisode !
Les questions de l’épisode !
La Terre sphérique :
- Qui a prouvé pour la première fois que la Terre était une sphère ?
- Comment prouver simplement que la Terre est une sphère ?
Jouez au quiz de l’épisode !
La Terre sphérique
Les notions importantes
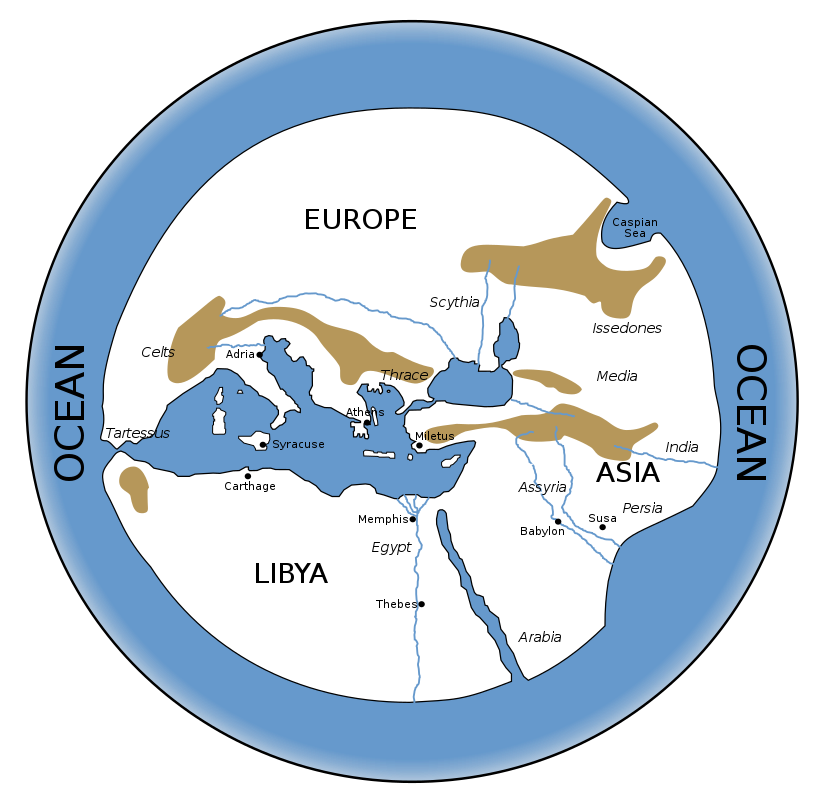
- L’une des plus anciennes cartes du monde date du VIème siècle av. J.C. et a été dessiné par le savant grec Anaximandre. Sa représentation du monde connu était parfaitement ronde, mais Anax’ pensait que la Terre était non pas sphérique, mais cylindrique ! Et que sa profondeur faisait un tiers de sa largeur.
- Les deux preuves importantes d’Aristote pour prouver une bonne fois pour toute que la Terre est une sphère sont les suivantes :
- L’éclipse lunaire. Le soleil projette l’ombre de la Terre sur la Lune. Et cette ombre est ronde !
- Les étoiles circumpolaires. Les étoiles circumpolaires ont une place différente quand on bouge sur le globe, voir même disparaissent totalement du champ de vision ! Ce serait une constatation impossible si la Terre était plate !
- Qu’est-ce qu’une étoile circumpolaire ? C’est une étoile qui, si l’on ne bouge pas, est toujours visible dans le ciel. Bien-sûr, si on voyage sur la Terre, cette étoile disparaît du champ de vision.
- Eratosthène a calculé la circonférence de la Terre de façon très simple et ingénieuse. Nous n’allons pas revenir ce que Jim a expliqué dans l’épisode, mais sur quelques notions clefs.
- Les rayons du soleil sont parallèles selon Eratosthène. Pourquoi ? Parce qu’il présume que le soleil est tellement éloigné de nous que les rares rayons solaires qui nous parviennent vont dans la même direction.
- Eratosthène connaît sa géométrie ! L’important théorème à retenir ici est celui des angles alternes-internes : quand deux lignes droites sont coupées en deux, leurs angles alternes-internes (ou leurs angles opposés si vous voulez) sont identiques.Vu que l’angle au sommet de la colonne à Alexandrie fait 7,2°, alors l’angle qui sépare la capitale égyptienne de Syène est aussi de 7,2°, soit 1/50ème de la circonférence totale d’un cercle.Il suffit donc de connaître la distance entre Syène et Alexandrie, et de la multiplier par 50.
- Il trouve 39,375 km. Quand on sait à quel point la mesure de la distance entre Alexandrie et Syène a été approximative, c’est presque un miracle qu’Eratosthène ait réussi à tomber si juste ! Puisqu’on estime que la circonférence de la Terre est d’environ 40,075 km.
Le quiz d’Une Tout Autre Histoire !
Le sphérico-quiz !
Bienvenue dans le quiz sur l'épisode "Aux Origines de la Terre sphérique" !
Bravo, vous avez terminé %%le questionnaire sur la Terre sphérique !%%.
Votre score est de %%SCORE%% sur %%TOTAL%%.
Votre performance : %%RATING%%
Vos réponses sont surlignées ci-dessous.